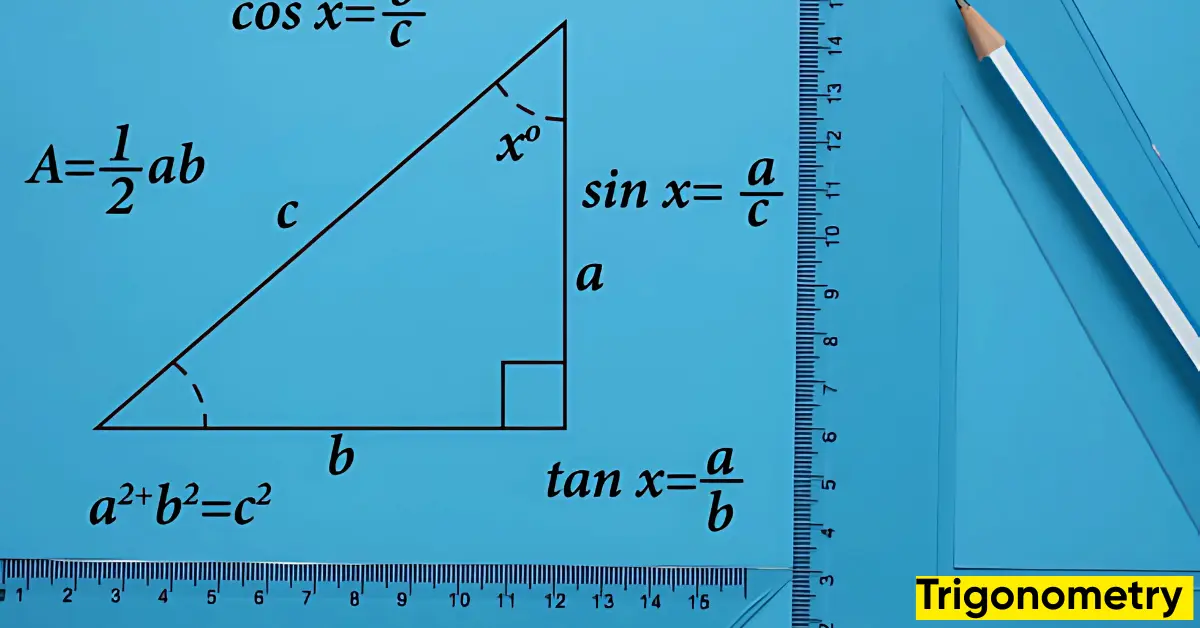Trigonometry Table, Formula, 0 to 360 Degree, Function and Example

What is Trigonometry?

Trigonometry is a part of math that deals with the angles and sides of triangles. It is useful in various fields, including engineering, physics, astronomy, and construction. One of the most important tools in trigonometry is the trigonometry table. This table shows the values of six trigonometric functions, sin, cos, tan, cot, sec, and cosec, for common angles such as 0°, 30°, 45°, 60°, and 90°. In this article, you will learn what a trigonometry table is, how it is made, and how it helps you solve questions in exams and real-life problems.

What Are Trigonometric Functions?

Before using the trigonometry table, it’s important to understand the basic trigonometric functions. These are used in a right-angled triangle to relate the sides to the angles.

• Sine (sin) – It is the ratio of the opposite side to the hypotenuse.
  Formula: sin θ = Opposite / Hypotenuse
• Cosine (cos) – It is the ratio of the adjacent side to the hypotenuse.
  Formula: cos θ = Adjacent / Hypotenuse
• Tangent (tan) – It is the ratio of the opposite side to the adjacent side.
  Formula: tan θ = Opposite / Adjacent

How to Construct a Trigonometry Table?

To calculate trig values manually:

1. Use special triangles (30°-60°-90° and 45°-45°-90°)
2. Apply Pythagoras’ theorem
3. Use quadrant rules:
   • Q1: All positive
   • Q2: Only sine (+)
   • Q3: Only tangent (+)
   • Q4: Only cosine (+)

Trigonometry Table from 0° to 360°

The trigonometry table helps you find the values of trigonometric functions like sin, cos, tan, cot, sec, and cosec for common angles between 0° and 360°. These values are used in solving triangles, geometry problems, and even physics equations. Here’s how the standard table looks:

Angle (°)	0°	30°	45°	60°	90°	180°	270°	360°
Angle (Radians)	0	π/6	π/4	π/3	π/2	π	3π/2	2π
sin θ	0	1/2	1/√2	√3/2	1	0	-1	0
cos θ	1	√3/2	1/√2	1/2	0	-1	0	1
tan θ	0	1/√3	1	√3	∞	0	∞	0
cot θ	∞	√3	1	1/√3	0	∞	0	∞
cosec θ	∞	2	√2	2/√3	1	∞	-1	∞
sec θ	1	2/√3	√2	2	∞	-1	∞	1

Applications of the Trigonometry Table?

The trigonometry table is a helpful tool used in many fields. It gives exact values of trigonometric functions like sin, cos, and tan for standard angles. Here are some common ways it’s used:

1. Solving Triangles
   The table helps in finding unknown sides or angles in right-angled triangles using known values of trigonometric functions.
2. Engineering and Physics
   Engineers and scientists use trigonometry to design machines, analyze motion, calculate forces, and build structures like bridges and buildings.
3. Astronomy and Navigation
   Astronomers use trigonometry to measure distances between stars and planets. Pilots and sailors use it to find direction and distance between locations.
4. Trigonometric Identities
   The values in the table help in learning and applying standard trigonometric identities that simplify complex math problems.
5. Calculus and Equations
   In advanced mathematics like calculus and differential equations, trigonometric functions are used to solve real-world problems involving waves, motion, and rates of change.
6. Wave and Signal Analysis
   Trigonometry helps in studying sound waves, light waves, and electronic signals. It is useful in fields like music, radio, and communication.

Advantages and Limitations of the Trigonometry Table

The trigonometry table is a helpful tool for students learning trigonometry. It offers a quick way to find values of trigonometric functions for commonly used angles and helps in solving basic to moderate-level problems. However, like any tool, it has its pros and cons depending on the use case.

Advantages

• Quick Reference: The table allows fast lookup of trigonometric values without needing a calculator, which is helpful during exams or concept learning.
• Ideal for Standard Angles: It provides exact values for key angles like 0°, 30°, 45°, 60°, 90°, etc., which are frequently used in problems.
• Builds Conceptual Understanding: Helps in developing a strong understanding of sine, cosine, tangent, and their relationships, especially for beginners.
• Supports Identity Practice: Knowing these values aids in simplifying trigonometric identities and solving related questions.
• Helpful in Exams: Especially useful for school and entrance exams where only standard angle values are often tested.

Limitations

• Limited Angle Coverage: It only includes specific angles (mostly multiples of 15 or 30), which means it’s not useful for odd or decimal angles like 17°, 73°, or 112.5°.
• No Flexibility for Real-Time Calculation: Unlike calculators, the table doesn’t allow users to compute values for any angle on the spot.
• Not Suitable for High-Precision Work: For engineering or advanced-level problems requiring high accuracy, the approximate values from the table may not be enough.
• Doesn’t Cover All Triangles: It’s mainly applicable to right-angled triangles and can’t directly solve non-right triangles without additional rules like Sine Rule or Cosine Rule.

Trigonometry Table and Functions -FAQs

---

• Puzzle Reasoning, Types, Strategies, Concepts, and Formulas
• Syllogism Reasoning, Strategies, Forms, Concepts, Tips & Tricks
• Top 10 Government Job Exams in India 2025, Complete List with Career Scope
• Important Days in November 2025, Holiday and Event List
• Important Days in October 2025, National and International Days
• Important Days in August 2025, Check Important Events

---