Tips and tricks to solve questions on percentages and ratios quickly

SBI PO and SSC CGL are around the corner. Percentages and ratios form the base for solving questions from many topics (data interpretation, age problems, simplification, etc.) and hence it becomes an important topic for quantitative section of any exam whether it is SSC, RRB or Banking. The questions based on these topics are usually easy and thus the speed of solving a question is based on how quickly you can solve these questions. In today’s blog we will be discussing on how to solve percentage questions quickly.

Solving ratio questions quickly: Important points

Ratio indicates how many times one number contains another.

Combined ratio from individual ratio

If A:B = a:b₁ and B:C = b₂:c then, A:B:C =(a*b₂):(b₁*b₂):(b₁*c)

Similarly,

If A:B = a:b₁, B:C = b₂:c₁ and C:D = c₂:d then, A:B:C:D = (a*b₂*c₂): (b₁*b₂*c₂):(b₁*c₁*c₂):(b₁*c₁*d)

Example: If A:B = 1:2, B:C = 3:7 and C:D = 4:5 then A:B:C:D =

Solution:

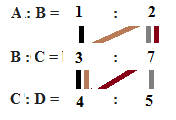
A:B:C:D = (1*3*4):(2*3*4):(2*7*4):(2*7*5) =12:24:56:70 = 6:12:28:35

If the difference between two quantities remains the same

Let us understand this concept through examples. This is helpful especially in age problems.

Example 1(Illustration): The ratio of number of boys to the number of girls in a school is 5:4. If 60 more students are admitted in the school such that the difference between number of boys and girls remains the same, the ratio becomes 13:11. What is the total number of students in the school?

Solution:

Initial ratio = 5:4, (Difference = 1)

Final ratio = 13:11, (Difference = 2)

The difference between number of boys and girls remains the same. Hence, the initial ratio should be multiplied by 2

Initial ratio * 2 =10:8, (Difference = 2)

Final ratio * 1 = 13:11, (Difference = 2)

Initially let number of boys = 10x then, number of girls = 8x

After the admission of 60 students, Number of boys = 13x and Number of girls = 11x

Since difference remains the same, Number of girls who were newly admitted to the school = Number of boys who were newly admitted to the school = 30

Number of girls who were newly admitted to the school = 11x – 8x = 3x = 30

x=10

Hence initially there was (10+8)x students = 180 students.

Example 2: Current age of father and daughter is in the ratio 2:1, while the current age of daughter and granddaughter is in the ratio of 8:1. If the age of father and daughter will be in the ratio 13:7 after 4 years, then what will be the age of the granddaughter after 4 years?

Solution:

Age of father and daughter

Initial ratio= (2:1)*(6:6) = 12:6

Final ratio = (13:7)*1 = 13:7

13x-12x = x = 4 years

Hence present age of daughter= 24 years

Present age of granddaughter = 24/8 = 3 years

Hence age of granddaughter after 4 years = 3+4 = 7 years

How to solve percentage questions quickly

Percentage is a number or ratio expressed as a fraction of 100. While solving problems, converting the percentages into fractions will save a lot of calculation and hence reduce the time required for solving. The table below depicts some percentages to fractions conversion:

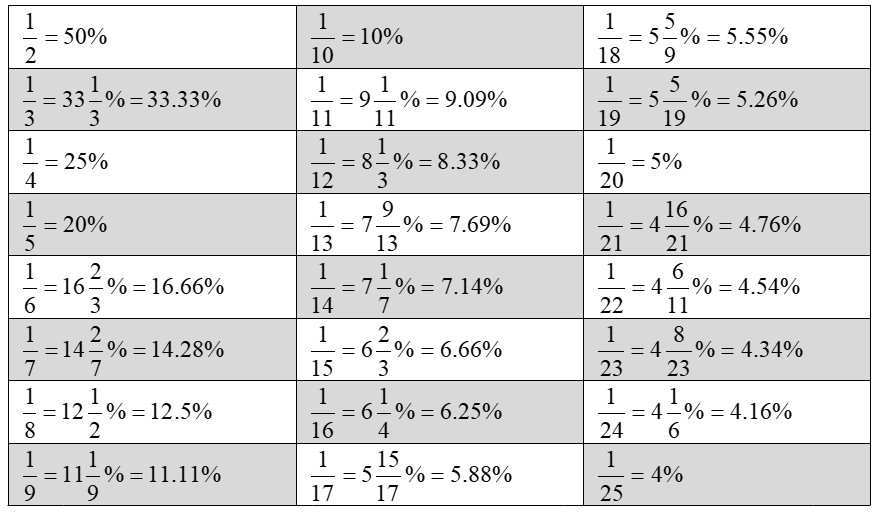
Apart from the above table, the following points are also important.

Successive increase or decrease

This is helpful for profit and loss, problems on depreciations, etc.

In case of successive increase or decrease of x% and y% respectively, we have

Effective increase or decrease = {(100 + x)/100 * (100+y)/100 – 1} * 100% = x + y + (x*y)/100

NOTE: Increase is represented as +ve and decrease as –ve

Similarly,

In case of successive increase or decrease of x%, y% and z% respectively, we have

Effective increase or decrease = {(100 + x)/100 * (100 + y)/100 * (100 + z)/100 – 1} * 100%

Example: A seller offers two successive discounts of 6.25% and 20% on a bag and is still able to earn 50% profit. If he offers only a single discount of 40% on M.R.P, what will be his profit percentage?

Solution:

Let C.P of bag = Rs. 100

Then, S.P of bag = Rs. 150

Let M.R.P of bag = Rs. x

Effective discount = (-20) + (-6.25) + (-20)*(-6.25)/100 = –25 (-ve sign indicates decrease)

Effective discount percentage = 25%

x*(100 – 25)/100=150

x= Rs. 200

New S.P = 200 * (100 – 40)/100 =Rs. 120

Hence new profit = (120 – 100)/100 = 20%

Constant amount of commodity in mixture

For a commodity whose amount remains constant in a mixture

Quantity of new mixture * New % = Quantity of old mixture * Old %

Example: An alcohol water mixture contains 14.28% alcohol. If 40 litres of water is added to the mixture, the new mixture contains 9.09% of alcohol. What was the quantity of initial mixture?

Solution:

14.28% = 1/7 and 9.09% = 1/11

Let the initial quantity be y

(y+40)*1/11=y*1/7

y=70 litres

Increase or decrease in consumption

For expenditure to be constant when price increases/decreases by r%

Increase or decrease in consumption =│r│/(100 + r) * 100, │r│→modulus of r

Example: Price of sugar decreases by 20% then, by how much percentage the consumption should be increased so that expenditure remains constant?

Solution:

Increase in consumption = │(-20)│/(100 + (-20)) * 100 = 25% (-ve sign represents decrease)

We hope this post helped you and gave some new tricks on how to solve percentage questions quickly as well as questions on ratios quickly. Practice more and more problems based on these tricks to get acquainted with it. All the best for your examination!

Study at your own convenience anywhere. Download the Oliveboard app now!

FAQs