In the SSC CGL Tier 2 Statistics Paper SSC JSO, Analysis of Variance (ANOVA) is an important topic under Statistical Inference. It helps in comparing the means of multiple groups to see if there is any significant difference among them. This article explains the concept of ANOVA, its assumptions, types (One-way and Two-way classification), formulas, and examples in an easy-to-understand manner.
What is Analysis of Variance (ANOVA)?
Analysis of Variance (ANOVA) is a statistical technique used to test whether the means of three or more groups are significantly different. While t-tests compare means of two groups, ANOVA extends this concept to more than two groups. It works by analyzing the variation between groups and within groups.
Also check out Most Repeated Quantitative Aptitude Questions for SSC CGL Tier 2
Basic Idea Behind ANOVA
ANOVA compares:
- Between-group variation (difference in means of different groups)
- Within-group variation (difference within each group)
If the between-group variation is much larger than the within-group variation, it means at least one group mean is significantly different.
Check out Most Repeated Reasoning Questions for SSC CGL Tier 2
Key Terms used in ANOVA
Below are the terms used in ANOVA:
| Term | Meaning |
| Factor | The variable that divides the data into groups (e.g., teaching method) |
| Level | The different categories or groups under a factor (e.g., Method A, B, C) |
| Treatment | Each combination of factor and level |
| Sum of Squares (SS) | Measure of variation (explained or unexplained) |
| Mean Square (MS) | Average variation (SS divided by degrees of freedom) |
| F-statistic | Ratio of between-group to within-group variance |
Check out Most Repeated Computer Awareness Questions for SSC CGL Tier 2
Types of ANOVA
There are two main types of ANOVA for SSC CGL JSO exam:
- One-way ANOVA (Single factor classification)
- Two-way ANOVA (Two factor classification)
1. One-Way ANOVA (Single Factor Classification)
Definition
One-way ANOVA is used when there is only one independent variable (factor) and we want to test if the means of three or more groups are equal. For example: A teacher wants to test whether three different teaching methods (A, B, C) lead to different average marks among students.
Assumptions of One-Way ANOVA
- Samples are independent.
- Each group follows a normal distribution.
- All groups have equal variances (homogeneity of variance).
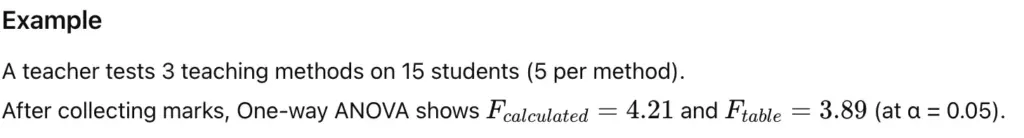
2. Two-Way ANOVA (Two Factor Classification)
Definition
Two-way ANOVA is used when there are two independent factors affecting one dependent variable, and each factor has two or more levels.
For example:
A researcher studies the effect of teaching method (A, B) and gender (Male, Female) on student marks.
Here:
- Factor 1: Teaching Method
- Factor 2: Gender
Purpose
Two-way ANOVA helps in studying:
- The individual effect of each factor.
- The combined (interaction) effect of both factors.
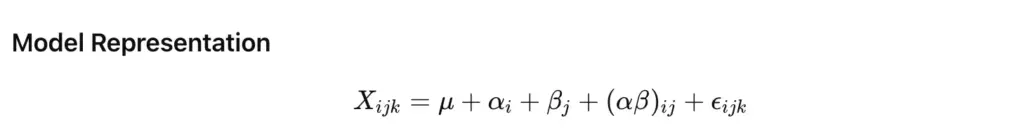
Assumptions of Two-Way ANOVA
- Samples are independent and normally distributed.
- Variance across all groups is equal.
- Observations are random.
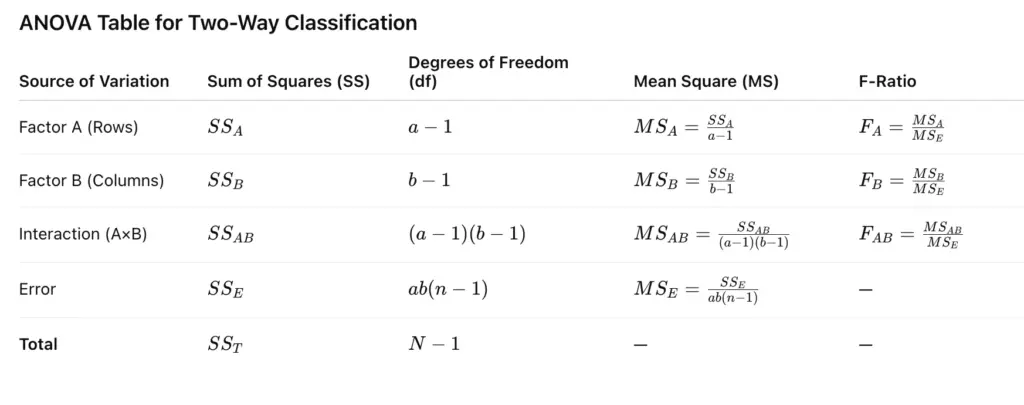
ANOVA Table for Two-Way Classification
Decision Rule
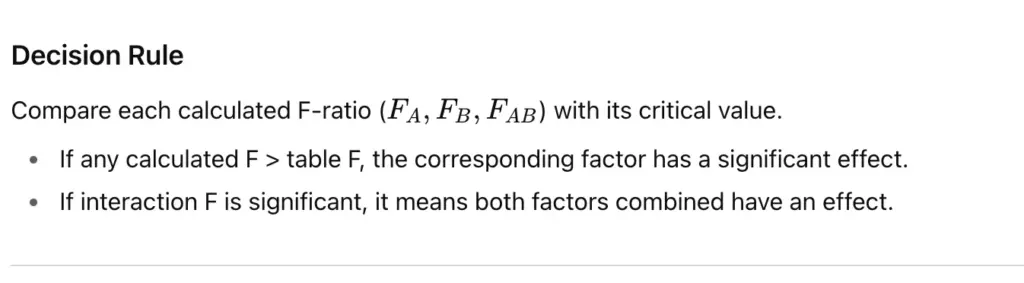
Example
A company wants to see if machine type (A, B) and operator experience (Skilled, Unskilled) affect production rate.
Two-way ANOVA shows:
- FA=5.8>Ftable=3.9F_A = 5.8 > F_{table} = 3.9FA=5.8>Ftable=3.9 → Machine type has significant effect.
- FB=2.5<3.9F_B = 2.5 < 3.9FB=2.5<3.9 → Experience has no significant effect.
- FAB=1.8<3.9F_{AB} = 1.8 < 3.9FAB=1.8<3.9 → No interaction effect.
Hence, only machine type affects production significantly.
Key Takeaways
- ANOVA is used to compare means of more than two groups.
- One-way ANOVA → One factor; Two-way ANOVA → Two factors.
- F-test is used to measure variation among group means.
- Assumptions: normality, independence, equal variances.
- Practice ANOVA questions from past SSC CGL JSO papers for better conceptual clarity.
Check other SSC JSO related blogs:
FAQs
To test if there are significant differences between the means of three or more groups.
One-way ANOVA studies one factor; Two-way ANOVA studies two factors and their interaction effect.
It is the ratio of variance between groups to variance within groups.
Normal distribution, independence of samples, and equal variances across groups.
Technically yes, but a t-test is preferred for comparing two groups.
- Most Expected Statistics MCQs with Solutions for SSC JSO Tier 2
- SSC JSO Books, Study Material, Preparation, Syllabus
- Index Numbers for SSC CGL Tier 2 for JSO Post
- Time Series Analysis for SSC CGL Tier 2, JSO Post
- Analysis of Variance (ANOVA) for SSC CGL Tier 2, Paper 2
- Statistical Inference for SSC CGL Tier 2, Paper 2
I’m Mahima Khurana, a writer with a strong passion for creating meaningful, learner-focused content especially in the field of competitive exam preparation. From authoring books and developing thousands of practice questions to crafting articles and study material, I specialize in transforming complex exam-related topics into clear, engaging, and accessible content. I have first hand experience of 5+ months in SSC Exams. Writing, for me, is not just a skill but a way to support and guide aspirants through their preparation journey one well-written explanation at a time.