Sampling Theory for SSC CGL Tier 2 Paper 2

Add as a preferred source on Google
Published on 17 October 2025 by

Last updated on October 27th, 2025 at 01:15 pm

In SSC CGL Tier 2, SSC JSO, Sampling Theory is an important part of Statistics. Understanding sampling helps in making inferences about a population using a sample. This blog covers population, sample, sampling techniques, errors, and sampling distributions with easy explanations.

1. Population and Sample

In statistics, understanding the difference between a population and a sample is fundamental, as it forms the basis for collecting data and making inferences about a larger group.

TermDefinitionExample
PopulationComplete set of items or individuals under studyAll employees of a company
SampleSubset of population selected for analysis100 employees selected randomly
Attempt Free New Interface SSC CGL Tier 2 Mock test

Also check out Most Repeated Quantitative Aptitude Questions for SSC CGL Tier 2

2. Sampling Techniques

Sampling techniques are divided into probability and non-probability methods.

TypeTechniqueDescriptionUse / Example
ProbabilitySimple Random SamplingEvery item has an equal chanceDrawing 50 names randomly
ProbabilitySystematic SamplingEvery kth item is selectedEvery 10th student in a list
ProbabilityStratified SamplingPopulation divided into strata, samples from eachSample of students by grade
ProbabilityCluster SamplingPopulation divided into clusters, select entire clustersRandomly select 3 schools
Non-ProbabilityConvenience SamplingSelect easily available itemsSurvey friends in a class
Non-ProbabilityJudgmental / PurposiveSelect based on researcher’s judgmentExpert opinion survey
Check SSC CGL Tier 2 Weightage of English and Quant

Also check out Most Repeated Quantitative Aptitude Questions for SSC CGL Tier 2

3. Sampling Errors

Sampling errors occur when a sample does not perfectly represent the population.

Error TypeDescriptionExample
Random ErrorDue to chance variation in sampleSelecting 100 students randomly may slightly differ from population mean
Systematic Error / BiasConsistent error in one directionSurvey conducted only in morning → misses absent students
Non-Sampling ErrorErrors not related to samplingData entry mistakes, misreporting

Check out Most Repeated Reasoning Questions for SSC CGL Tier 2

4. Sampling Distribution

Calculate your Score using sSC CGL Tier 1 Score Calculator

Check out Most Repeated Computer Awareness Questions for SSC CGL Tier 2

5. Key Formulas for SSC CGL

In SSC CGL Tier 2, memorizing key formulas for sampling theory helps quickly calculate sample statistics, standard errors, and make accurate inferences about the population.

Check SSC CGL Tier 2 Books

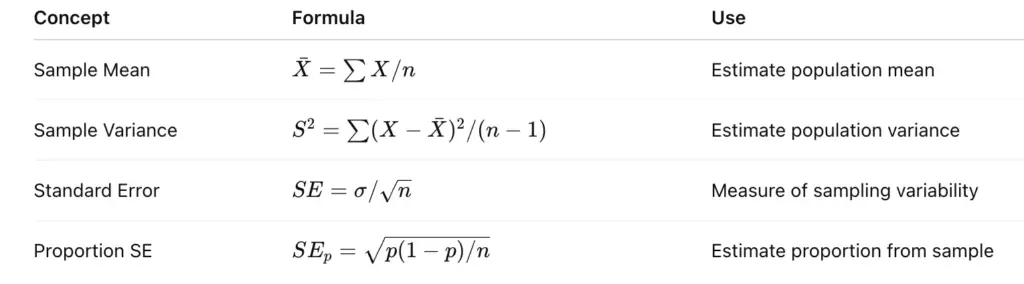
Key Takeaways

  • Population is the whole group, sample is a subset.
  • Probability sampling → each element has known chance; Non-probability → chance unknown.
  • Sampling errors can be random or systematic.
  • Sampling distribution → distribution of sample statistics; CLT allows normal approximation for large samples.
  • Standard error quantifies sample variability.

Check other SSC JSO related blogs:

BlogsBlogs
SSC JSO Mock TestSSC JSO Books
SSC JSO Cut OffSSC JSO Promotion

FAQs on Sampling Theory

Q1. What is the difference between population and sample?

Population is the whole group; sample is a subset used for analysis.

Q2. What is stratified sampling?

Divide population into strata and select samples from each stratum.

Q3. What is a sampling error?

Error due to difference between sample statistics and population parameters.

Q4. What is Central Limit Theorem?

For large sample size, the distribution of sample mean is approximately normal regardless of population shape.

Q3. What are the main types of sampling techniques?

Sampling techniques are of two main types:
Probability sampling – each element has a known chance of selection (e.g., random, stratified).
Non-probability sampling – selection based on convenience or judgment.