Measures of Dispersion for SSC CGL Tier 2 (JSO Post)

In SSC CGL Tier 2, especially for the Junior Statistical Officer (JSO) post, understanding Measures of Dispersion is very important. Dispersion shows how spread out the data is around the central value. While measures like Mean, Median, and Mode give a single representative value, dispersion helps us understand how consistent or varied the data is.

What is Dispersion?

Dispersion tells us how much the data values differ from each other or from the average.
In simple words, it measures the spread or variability in a data set. If all values are close to each other, dispersion is small. If values are far apart, dispersion is large.

Also check out Most Repeated Quantitative Aptitude Questions for SSC CGL Tier 2

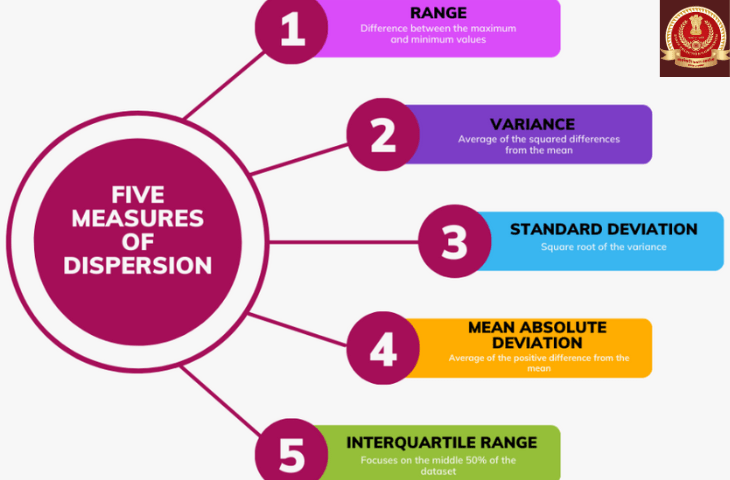
Types of Measures of Dispersion

The main types of measures of dispersion are:

Type of Measure	Definition	Formula / Method
Range	Difference between the largest and smallest value in a dataset.	Range = Largest Value − Smallest Value
Quartile Deviation (Q.D.)	Measures the spread of the middle 50% of data between Q₁ and Q₃.	Q.D. = (Q₃ − Q₁) / 2
Mean Deviation (M.D.)	Average of absolute deviations from the mean, median, or mode.	M.D. = (Σ
Standard Deviation (S.D.)	Square root of average of squared deviations from the mean.	S.D. = √(Σ(x − 𝑥̄)² / N)
Relative Measures of Dispersion	Expresses dispersion as a percentage or ratio for comparison.	– Coefficient of Range = (L − S)/(L + S) – Coefficient of Q.D. = (Q₃ − Q₁)/(Q₃ + Q₁) – Coefficient of M.D. = M.D./Mean – Coefficient of Variation (C.V.) = (S.D./Mean) × 100

Also check out Most Repeated Quantitative Aptitude Questions for SSC CGL Tier 2

1. Range

Definition:
Range is the simplest measure of dispersion. It is the difference between the highest and lowest values in a data set.

Formula: Range=Maximum Value−Minimum Value\text{Range} = \text{Maximum Value} – \text{Minimum Value}Range=Maximum Value−Minimum Value

Example:
If marks in a test are 25, 35, 40, 50, and 60, then
Range = 60 – 25 = 35

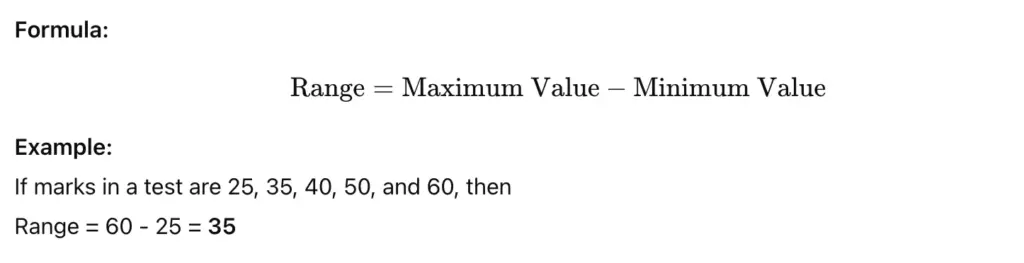
Use:
Range gives a quick idea about the spread of data but is affected by extreme values.

2. Quartile Deviation (QD)

Definition:
Quartile Deviation, also called Semi-Interquartile Range, measures the spread of the middle 50% of data.

Formula: Quartile Deviation (QD)=Q3−Q12\text{Quartile Deviation (QD)} = \frac{Q_3 – Q_1}{2}Quartile Deviation (QD)=2Q3​−Q1​​

where,
Q1Q_1Q1​ = First Quartile (25th percentile)
Q3Q_3Q3​ = Third Quartile (75th percentile)

Example:
If Q1=40Q_1 = 40Q1​=40 and Q3=60Q_3 = 60Q3​=60, QD=60−402=10QD = \frac{60 – 40}{2} = 10QD=260−40​=10

Use:
Quartile Deviation is less affected by extreme values and is useful when data has outliers.

Check out Most Repeated Reasoning Questions for SSC CGL Tier 2

3. Mean Deviation (MD)

Definition:
Mean Deviation shows the average of absolute deviations of values from a central point (mean, median, or mode).

Formula: Mean Deviation=∑∣x−xˉ∣N\text{Mean Deviation} = \frac{\sum |x – \bar{x}|}{N}Mean Deviation=N∑∣x−xˉ∣​

where,
xxx = each observation,
xˉ\bar{x}xˉ = mean,
NNN = number of observations.

Example:
If the data is 2, 4, 6, 8, 10,
Mean xˉ=6\bar{x} = 6xˉ=6
Mean Deviation = (|2-6| + |4-6| + |6-6| + |8-6| + |10-6|) / 5 = (4 + 2 + 0 + 2 + 4)/5 = 2.4

Use:
It shows average variation in the data and is better than range as it considers all observations.

Check out Most Repeated Computer Awareness Questions for SSC CGL Tier 2

4. Standard Deviation (SD)

Definition:
Standard Deviation is the most commonly used and accurate measure of dispersion. It measures how much each value deviates from the mean.

Formula: σ=∑(x−xˉ)2N\sigma = \sqrt{\frac{\sum (x – \bar{x})^2}{N}}σ=N∑(x−xˉ)2​​

Example:
If data = 2, 4, 6, 8, 10,
Mean xˉ=6\bar{x} = 6xˉ=6
SD σ=(2−6)2+(4−6)2+(6−6)2+(8−6)2+(10−6)25\sigma = \sqrt{\frac{(2-6)^2 + (4-6)^2 + (6-6)^2 + (8-6)^2 + (10-6)^2}{5}}σ=5(2−6)2+(4−6)2+(6−6)2+(8−6)2+(10−6)2​​
= √(40/5) = √8 = 2.83

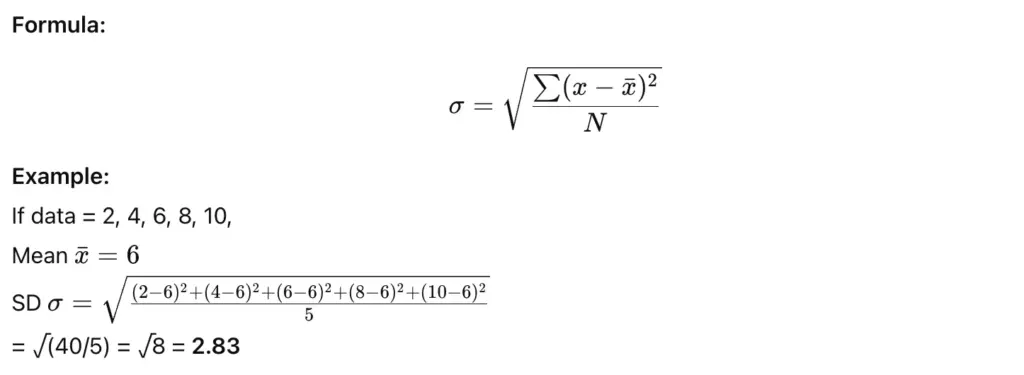
Use:
It is widely used in statistics as it considers all values and shows how data varies around the mean.

5. Relative Measures of Dispersion

Definition:
Relative dispersion compares the spread of two or more data sets, making it dimensionless.

Common relative measures include:

• Coefficient of Range
• Coefficient of Quartile Deviation
• Coefficient of Mean Deviation
• Coefficient of Standard Deviation (also called Coefficient of Variation)

Measure	Formula
Coefficient of Range	(Max – Min) / (Max + Min)
Coefficient of Quartile Deviation	(Q3 – Q1) / (Q3 + Q1)
Coefficient of Mean Deviation	Mean Deviation / Mean
Coefficient of Variation (CV)	(Standard Deviation / Mean) × 100

Use:
It helps compare the stability or consistency between different data sets. A lower CV means more consistency.

Comparison of Different Measures of Dispersion

Measure	Formula	Key Feature
Range	Max – Min	Simplest, affected by extremes
Quartile Deviation	(Q3 – Q1)/2	Based on middle 50% data
Mean Deviation	∑	x – mean
Standard Deviation	√(∑(x – mean)² / N)	Most accurate and reliable
Coefficient of Variation	(SD/Mean) × 100	Used for comparing data sets

Key Takeaways

Below are the key takeaways:

• Dispersion shows how data values vary around a central point.
• Standard Deviation is the most reliable measure used in SSC CGL Tier 2.
• Range is simple but less accurate due to outliers.
• Relative dispersion helps compare the variability between data sets.
• Practice numerical problems from each topic for JSO Paper 2 to build accuracy and speed.

Check out SSC CGL Exam Pattern

FAQs

---

• Sampling Theory for SSC CGL Tier 2 Paper 2
• Correlation and Regression SSC CGL Tier 2 Paper 2
• Moments, Skewness, and Kurtosis for SSC CGL Tier 2 Paper 2
• Measures of Dispersion for SSC CGL Tier 2 (JSO Post)
• Measures of Central Tendency for SSC CGL Tier 2, Paper 2
• Important Statistics Topics for SSC CGL Tier 2, Check Details Here

---