Height and Distance is one of the most visual and scoring topics in Quantitative Aptitude. It primarily involves the application of trigonometric ratios to calculate heights, distances, and angles in real-life or exam-based scenarios. In this blog we have provided all the details about height and distance, important formulas, tricks, types of questions, solved examples from 2024–25 exams.
What Is Height and Distance in Quantitative Aptitude?
Height and Distance refers to problems that involve measuring the vertical height of an object or the horizontal distance between two points, using the concept of angles of elevation and depression in trigonometry.
In competitive exams, these questions test a candidate’s visualization skills, trigonometric knowledge, and problem-solving speed.
Skills Required:
- Understanding of basic trigonometric ratios (sin, cos, tan)
- Ability to draw diagrams from word problems
- Logical sequencing of given data
Why Is Height and Distance Important in Competitive Exams?
Height and Distance is a high-scoring topic because it often appears as a single, straightforward question in the Quantitative Aptitude section.
| Exam | No. of Questions | Difficulty |
| SSC CGL / CHSL | 1–2 | Easy |
| IBPS PO / SBI PO | 1–2 | Moderate |
| RRB NTPC / Group D | 1 | Easy |
| State PSC / Police | 1–2 | Moderate |
Height and Distance Quantitative Aptitude Short Notes
Height and Distance questions use angles of elevation and depression along with trigonometric formulas to calculate unknown measures.
| Term | Definition |
| Angle of Elevation | Angle between the horizontal line and the line of sight to an object above the horizontal level. |
| Angle of Depression | Angle between the horizontal line and the line of sight to an object below the horizontal level. |
| Line of Sight | The imaginary line drawn from the observer’s eye to the object. |
| Horizontal Distance | The straight-line distance along the ground between two points. |
| Vertical Height | The perpendicular height from the base to the top of the object. |
Height and Distance Quick Revision Summary
The quick revision concepts for the topic Height and Distance are as follows:
| Concept | Explanation |
| Tan θ | Opposite side / Adjacent side |
| Sin θ | Opposite side / Hypotenuse |
| Cos θ | Adjacent side / Hypotenuse |
| Angle of Elevation | Eye looking upward to see an object |
| Angle of Depression | Eye looking downward to see an object |
| Common Exam Ratios | sin 30° = 1/2, cos 60° = 1/2, tan 45° = 1 |
What Are the Types of Height and Distance Questions in Quantitative Aptitude?
In exams, Height and Distance questions can be asked in various forms such as:
- Direct – Straightforward application of trigonometric ratios.
- Two-step problems – Using multiple angles or heights in a single problem.
- Object movement – Object changes position and alters the angle of elevation.
- Mixed-concept – Combined with time-speed-distance or geometry.
Height and Distance Formulas for Quantitative Aptitude
The formulas used to solve height and distance questions are as follows:
- tan θ = Opposite / Adjacent
- sin θ = Opposite / Hypotenuse
- cos θ = Adjacent / Hypotenuse
Height and Distance Tricks for SSC CGL and Other Exams
Tricks to solve height and distance questions in less time are as follows:
- Always draw a diagram before solving.
- Label all given angles and distances clearly.
- Remember tan = height / distance for most cases.
- Memorise standard trigonometric values (0°, 30°, 45°, 60°, 90°).
- In two-angle problems, solve step by step — do not combine prematurely.
Solved Height and Distance Questions from 2024–25 Exams
Q1. (SSC CGL 2024 Tier 1 Shift 2 – Memory Based)
The angle of elevation of the top of a tower from a point 60 m away from its base is 30°. Find the height of the tower.
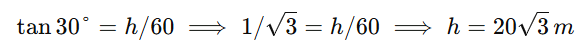
Q2. (IBPS PO Prelims 2024 – Based on Memory)
A man observes the top of a building at 45° angle of elevation. After walking 20 m towards the building, the angle becomes 60°. Find the height of the building.
Solution: Use two-tan formula and solve: Height = 20 m.
Q3. (RRB NTPC 2024)
From the top of a 50 m tower, the angle of depression of an object on the ground is 30°. Find the horizontal distance.
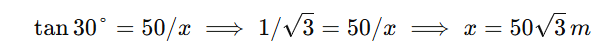
Height and Distance Concepts for Bank Exams
In IBPS/SBI exams, Height and Distance is often merged with time-speed-distance or boat-stream problems.
Example: A balloon rises at 5 m/s and is observed at a certain angle from a moving point — calculate the distance after a given time. These require both trigonometry and relative speed concepts.
Common Mistakes to Avoid while Solving Height and Distance Questions
Common mistakes to avoid while solving questions based on height and distance are as follows:
- Not drawing a diagram leads to misinterpretation.
- Confusing angle of elevation with depression – always check direction.
- Mixing up base and height in tan/sin/cos formulas.
- Forgetting to convert units (meters, kilometers).
- Skipping standard value memorization wastes time in calculation.
FAQs
Draw the figure, mark known angles/distances, and apply the correct trigonometric ratio without extra steps.
Mainly:
tan θ = Opposite / Adjacent
sin θ = Opposite / Hypotenuse
cos θ = Adjacent / Hypotenuse
Pythagoras theorem for right-angled triangles.
Yes, you must know basic ratios and standard angle values (0°, 30°, 45°, 60°, 90°).
Commonly used:
sin 30° = 1/2, cos 30° = √3/2, tan 30° = 1/√3
sin 45° = 1/√2, cos 45° = 1/√2, tan 45° = 1
sin 60° = √3/2, cos 60° = 1/2, tan 60° = √3
Elevation: looking up at an object.
Depression: looking down at an object.
- Height and Distance Question Types, Formulas, Short Tricks and Tips
- RRB Paramedical Preparation Strategy 2025, Study Plan & Tips
- Sentence Improvement Question Types, Concepts and Tricks
- Partnership Question Types, Formulas, Short Tricks and Tips
- Profit and Loss Formulas, Concepts, Short Tricks and Tips
- Problems Based on Trains Question Types, Short Tricks
Hello, I’m Aditi the creative mind behind the words at Oliveboard. As a content writer specializing in state-level exams, my mission is to simplify complex exam information and help aspirants navigate their journey with clarity and confidence.
Having walked the path of an aspirant myself, I bring a unique, relatable perspective to my work. I focus on crafting accessible and accurate content on Exam Notifications, Admit Cards, and Results, ensuring candidates have the right information at the right time.
At Oliveboard, I play a key role in empowering students by breaking down the exam process into understandable and actionable insights. My aim is to make preparation less daunting and more rewarding, one well-informed step at a time.