Measures of Dispersion for SSC CGL Tier 2 (JSO Post)

Add as a preferred source on Google
Published on 17 October 2025 by

Last updated on October 21st, 2025 at 06:24 pm

In SSC CGL Tier 2, especially for the Junior Statistical Officer (JSO) post, understanding Measures of Dispersion is very important. Dispersion shows how spread out the data is around the central value. While measures like Mean, Median, and Mode give a single representative value, dispersion helps us understand how consistent or varied the data is.

What is Dispersion?

Dispersion tells us how much the data values differ from each other or from the average.
In simple words, it measures the spread or variability in a data set. If all values are close to each other, dispersion is small. If values are far apart, dispersion is large.

Attempt Free New Interface SSC CGL Tier 2 Mock test

Also check out Most Repeated Quantitative Aptitude Questions for SSC CGL Tier 2

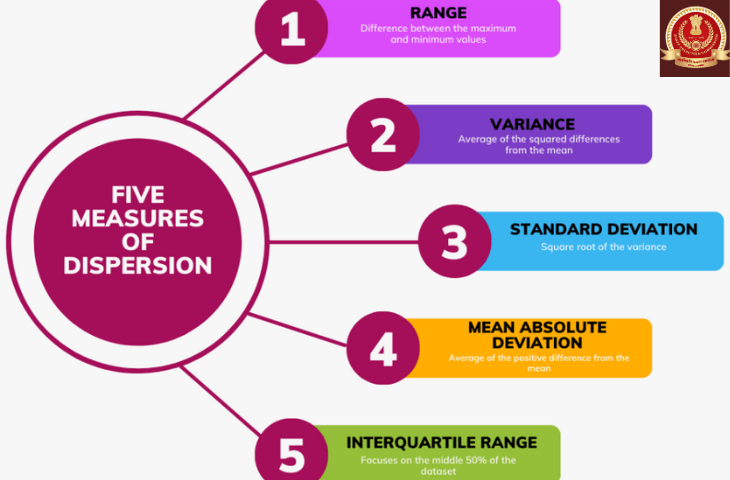
Types of Measures of Dispersion

The main types of measures of dispersion are:

Type of MeasureDefinitionFormula / Method
RangeDifference between the largest and smallest value in a dataset.Range = Largest Value − Smallest Value
Quartile Deviation (Q.D.)Measures the spread of the middle 50% of data between Q₁ and Q₃.Q.D. = (Q₃ − Q₁) / 2
Mean Deviation (M.D.)Average of absolute deviations from the mean, median, or mode.M.D. = (Σ
Standard Deviation (S.D.)Square root of average of squared deviations from the mean.S.D. = √(Σ(x − 𝑥̄)² / N)
Relative Measures of DispersionExpresses dispersion as a percentage or ratio for comparison.– Coefficient of Range = (L − S)/(L + S) – Coefficient of Q.D. = (Q₃ − Q₁)/(Q₃ + Q₁) – Coefficient of M.D. = M.D./Mean – Coefficient of Variation (C.V.) = (S.D./Mean) × 100
Check SSC CGL Tier 2 Weightage of English and Quant

Also check out Most Repeated Quantitative Aptitude Questions for SSC CGL Tier 2

1. Range

Definition:
Range is the simplest measure of dispersion. It is the difference between the highest and lowest values in a data set.

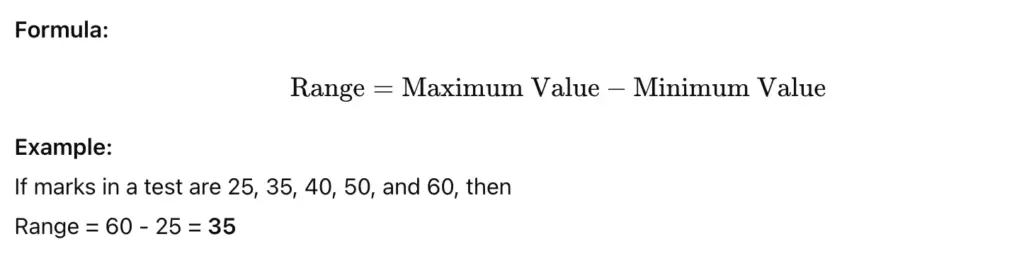
Use:
Range gives a quick idea about the spread of data but is affected by extreme values.

2. Quartile Deviation (QD)

Definition:
Quartile Deviation, also called Semi-Interquartile Range, measures the spread of the middle 50% of data.

Use:
Quartile Deviation is less affected by extreme values and is useful when data has outliers.

Check out Most Repeated Reasoning Questions for SSC CGL Tier 2

3. Mean Deviation (MD)

Definition:
Mean Deviation shows the average of absolute deviations of values from a central point (mean, median, or mode).

Use:
It shows average variation in the data and is better than range as it considers all observations.

Calculate your Score using sSC CGL Tier 1 Score Calculator

Check out Most Repeated Computer Awareness Questions for SSC CGL Tier 2

4. Standard Deviation (SD)

Definition:
Standard Deviation is the most commonly used and accurate measure of dispersion. It measures how much each value deviates from the mean.

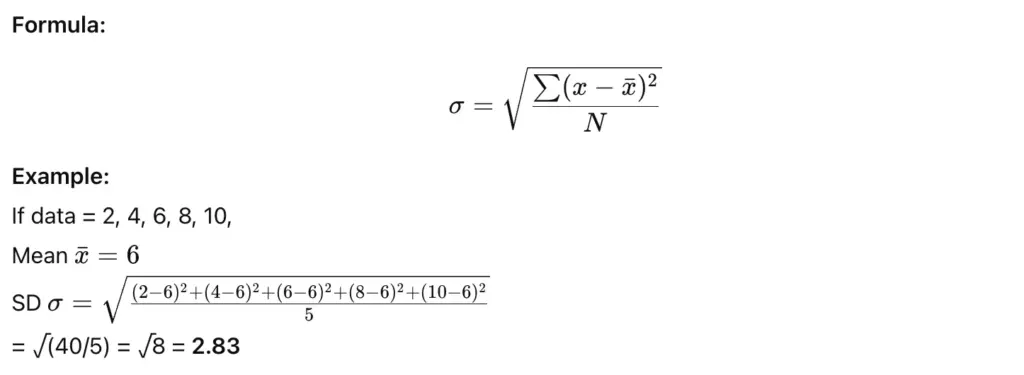
Use:
It is widely used in statistics as it considers all values and shows how data varies around the mean.

Check SSC CGL Tier 2 Books

5. Relative Measures of Dispersion

Definition:
Relative dispersion compares the spread of two or more data sets, making it dimensionless.

Common relative measures include:

  • Coefficient of Range
  • Coefficient of Quartile Deviation
  • Coefficient of Mean Deviation
  • Coefficient of Standard Deviation (also called Coefficient of Variation)
MeasureFormula
Coefficient of Range(Max – Min) / (Max + Min)
Coefficient of Quartile Deviation(Q3 – Q1) / (Q3 + Q1)
Coefficient of Mean DeviationMean Deviation / Mean
Coefficient of Variation (CV)(Standard Deviation / Mean) × 100

Use:
It helps compare the stability or consistency between different data sets. A lower CV means more consistency.

SSC CGL Tier 2 Previous Year Paper, Download Free PDF

Comparison of Different Measures of Dispersion

MeasureFormulaKey Feature
RangeMax – MinSimplest, affected by extremes
Quartile Deviation(Q3 – Q1)/2Based on middle 50% data
Mean Deviation∑x – mean
Standard Deviation√(∑(x – mean)² / N)Most accurate and reliable
Coefficient of Variation(SD/Mean) × 100Used for comparing data sets

Check other SSC JSO related blogs:

BlogsBlogs
SSC JSO Mock TestSSC JSO Books
SSC JSO Cut OffSSC JSO Promotion

Key Takeaways

Below are the key takeaways:

  • Dispersion shows how data values vary around a central point.
  • Standard Deviation is the most reliable measure used in SSC CGL Tier 2.
  • Range is simple but less accurate due to outliers.
  • Relative dispersion helps compare the variability between data sets.
  • Practice numerical problems from each topic for JSO Paper 2 to build accuracy and speed.

Check out SSC CGL Exam Pattern

Attempt SSC CGL Tier 2 Live Test Here

FAQs

Q1. What is the easiest measure of dispersion?

Range is the simplest and quickest measure of dispersion.

Q2. Which measure of dispersion is used most in SSC CGL Tier 2 JSO Paper?

Standard Deviation is most used because of its accuracy and importance in data analysis.

Q3. What is the difference between Absolute and Relative Dispersion?

Absolute measures (like SD, MD) use actual units, while Relative measures (like CV) use ratios or percentages.

Q4. What does a low Coefficient of Variation mean?

It means data is more consistent or stable.

Q5. Why are dispersion measures important in SSC CGL JSO Paper 2?

They help in understanding variability, data interpretation, and solving statistical problems quickly and accurately.