Quantitative Aptitude for SSC: Congruence and similarity of triangles

Geometry is an important topic of Quantitative Aptitude in SSC. To become proficient in this topic, a candidate should develop a good command over the basics, theorems, and applications. In this blog, we will be discussing about the congruence and similarity of triangles for SSC which is a subtopic of Geometry for SSC.

Congruence and similarity of triangles for SSC

• Two triangles are said to be congruent if they have the same shape and size. In other words, two triangles are congruent if their corresponding sides and corresponding angles are equal.
• Two triangles are said to be similar if they have same shape. In other words, two triangles are similar if their corresponding angles are equal and their corresponding sides are proportional.

 CPCTC: Corresponding Parts of Congruent Triangles are Congruent

Ace the Numerical Ability section with the help of Oliveboard

Conditions for Congruence of Triangles

1. SSS (Side-Side-Side):

Corresponding sides are equal.

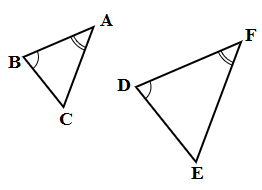
In △ABC and △DEF,

AB = FE, BC = ED and DF = CA

Hence △ABC ≅ △FED

Attempt a FREE SSC mock test here.

2. SAS (Side-Angle-Side):

Two corresponding sides and the corresponding angle between them are equal.

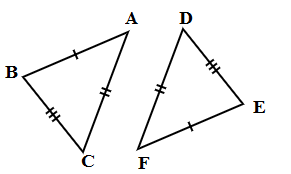
In △ABC and △DEF,

AB = FE, DF = CA and ∠A = ∠F

Hence △ABC ≅ △FED

3. AAS(Angle-Angle-Side):

Two corresponding angles and the corresponding side which is not between them are equal.

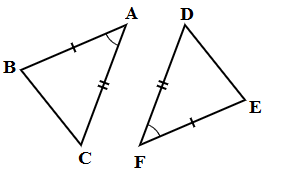
In △ABC and △DEF,

AB = FE, ∠C = ∠D and ∠A = ∠F

Hence △ABC ≅ △FED

Attempt a FREE SSC CHSL mock teste here

4. ASA (Angle-Side-Angle):

Two corresponding angles and the corresponding side between them are equal.

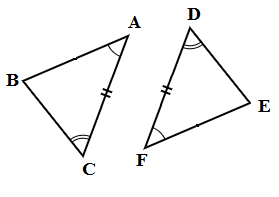
In △ABC and △DEF,

AC = FD, ∠C = ∠D and ∠A = ∠F

Hence △ABC ≅ △FED

5. RHS (Right-Hypotenuse-Side):

Hypotenuse and a pair of corresponding angles are equal in two right triangles.

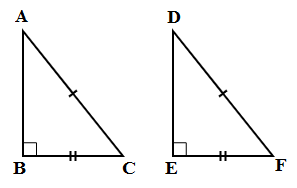
In △ABC and △DEF,

∠B = ∠E = 90⁰, AC = DF and BC = EF

Hence △ABC ≅ △DEF

Practice questions of Geometry for SSC exams, click here.

Conditions for Similarity of Triangles

1. AA (Angle-Angle):

Two pairs of corresponding angles are equal.

△ABC and △FDE are similar

2. SAS (Side-Angle-Side):

Two pairs of corresponding sides are proportional and the angle between them is equal.

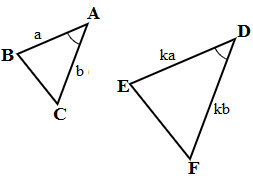
△ABC and △DEF are similar

3. SSS (Side-Side-Side):

Corresponding sides are proportional.

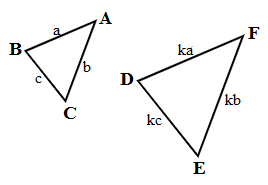
AB/FD = BC/DE = AC/FE

△ABC and △FDE are similar

 

Note: If two triangles are similar then,

1. Ratio of area of the two triangles = Ratio of squares of corresponding sides

2. Ratio of sides of two triangles

= Ratio of their heights/altitudes

= Ratio of their medians

= Ratio of their angle bisectors

= Ratio of their in-radii/circum-radii

= Ratio of their perimeters

The conditions given above form the backbone for the preparation Congruence and similarity of triangles for SSC exams. Learning them is a must! Let us look at some theorems based on Congruence and similarity of triangles for SSC exams.

Ace the Numerical Ability section with the help of Oliveboard

Congruence and similarity of triangles for SSC: Some Important Theorems

1. Basic Proportionality Theorem:

A line parallel to a side of a triangle divides the other two sides in the same ratio.

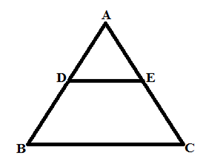
If DE ││ BC then,

AD/DB = AE/EC 

Example: Area of quadrilateral DECB is 180 cm² and DE divides AC in the ratio 2:5. If DE ││ BC, what is the area of △ADE?

a) 16 cm²

b) 32 cm²

c) 40 cm²

d) 20 cm²

Answer key: a

Solution:

AE/EC = 2/5 (DE divides AC in the ratio 2:5)

AE/EC = AD/DB (Basic Proportionality Theorem)

=> AE/EC = AD/AB = 2/7 and ∠DAE =∠BAC

=> △ADE and △ABC are similar. (By SAS Similarity Rule)

Area of △ADE / Area of △ABC = (2/7)² = 4/49

Let area of △ADE = 4x then, area of △ABC = 49 x

Area of △ABC = Area of △ADE + Area of quadrilateral DCEB

49 x = 4x + 180

45 x = 180

x = 4

Area of △ADE = 4 x = 16 cm²

Attempt a FREE SSC CGL mock test here.

2. Angle Bisector Theorem:

The angle bisector divides the side in the ratio of remaining two sides.

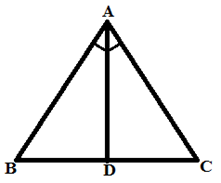
If AD bisects ∠A then, BD/DC = AB/AC

Example: If AD bisects ∠BAC and AD divides BC in the ratio 1:1 then, the ratio of area of △ABC to the area of △ABD is:

a) 3:1

b) 4:1

c) 3:2

d) 2:1

Answer key: d

Solution:

BD/DC = AB/AC = 1

=> AB = AC and BD = DC

Also, AD = AD (common side)

△ABD ≅ △ACD (By SSS Congruence Rule)

Area of △ABC = Area of △ABD + Area of △ACD

= 2 Area of △ABD (Since, area of congruent triangles are equal)

Required ratio = 2:1

Practice more questions on Congruence and similarity of triangles for SSC to become proficient in this topic. Also, don’t forget to solve previous year question papers.

All the best for your examination!

Crack any SSC exam or Railways exam- Register with Oliveboard now!

Study at your own convenience anywhere. Download the Oliveboard app now!