Mixture and alligation problems are asked in almost every exam, whether it is Banking, SSC, Railways, or any other banking exams. In prelims or phase 1, word problems from this topic can be 2-3 while in mains concept of mixture and alligation can be asked in Data Interpretation and Data sufficiency as well.
Questions in this section are a bit tricky to solve and usually we apply the concepts and formulas of weighted average, percentages and ratios to solve such questions. But these questions can also be solved using the concept of alligation and in this article we will discuss the detailed concept of mixture and alligation.
Register Here to Take A Free Mock Test Now
For Free Practice Questions on Mixture and Alligations Register here.
Understanding the Concept of Mixture and Alligation
Mixture: When two or more ingredients are mixed, mixtures can be of two types:
- Simple mixture: Formed after mixing two or more different ingredients.
- Complex mixture: Formed after mixing two or more different mixtures.
Rule of Alligation
The rule enables us to find the ratio in which two or more ingredients/mixture of different prices/concentration are mixed together to form a final mixture or desired price or concentration. Two methods are used:
Method 1 (formula method): It is given as-
Method 2 (Diagram method): The above method can be expressed using a diagram which will be more convenient to understand-
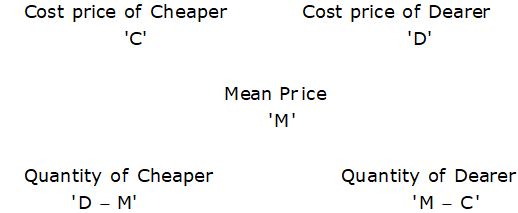
Note:
This rule of allegation can be applied to other topics such as profit and loss, average, percentage, simple interest/compound interest, ratio, and proportion.
Register here for free Study Material PDFs.
Alligation in Mixture Problems
We will see how the rule of allegation can be applied in mixture problems-
Example 1: A shopkeeper mixes 30 kg of type A rice of Rs.40/kg and 45 kg of type B rice of Rs.30/kg, then find the price of formed mixture of rice.
Solution:
By the rule of alligation:
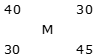
(30 – M): (M – 40) = 30: 45 = 2: 3
90 – 3M = 2M – 80
5M = 170
M = 34
Hence, price of mixture = Rs.34/kg
Note: After applying the concept of alligation on the price of the item of concentration of mixture we will get the ratio in which these two items or mixture are mixed.
Example 2: Mixture A of milk and water contains 75% milk and mixture B of milk and water contains 10% water, then find the ratio in which these two mixtures are mixed to form a third mixture which contains 15% water in it.
Solution:
Water percent in mixture A = 100% – 75% of 25%
By the rule of alligation:
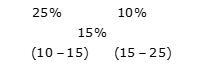
Required ratio = -5: -10
= 1: 2
Be exam ready with our Math Coach Feature – Try it for Free Here
Read Here to Find Tips and Tricks to Increase your Calculation Speed
Alligation in Profit and Loss Problems
It is used to find the overall profit or loss percent when cost prices of two items and profit/loss percent on the items are given-
Example 3: A shopkeeper sells type A rice at 20% profit and type B rice at 15% loss. If overall he earns 13% profit, then find the cost price of type A rice to type B rice.
Solution:
By the rule of alligation:
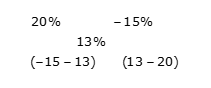
The ratio of the cost price of type A to type B rice = -28: -7
= 4: 1
Note: After applying alligatiion concept in profit/loss percent earned on the items we will get the ratio of cost prices of the items.
Put ‘–’ sign when loss percent is given.
Example 4: A shopkeeper purchased a table for Rs.1200 and sold it at 20% profit, he purchased a chair at Rs.400 and sold it at 10% profit, the find the overall profit percent earned by him.
Solution:
Let overall profit percent = M%
By the rule of alligation:
(10 – M): (M – 20) = 1200: 400 = 3: 1
10 – M = 3M – 60
4M = 70
M = 17.5
Hence, overall profit percent = M = 17.5%
Register here for FREE Study Material and Practice Questions PDFs.
Alligation in Speed, distance, and Time Problems
The concept of mixture and alligation can be used to find the average speed of journey-
Example 5: A person covers the first 3 hours of a journey with a speed 80 km/h and the remaining 5 hours with a speed 56 km/h, then find his average speed of the journey.
Solution:
Let average speed = X
By the rule of alligation:
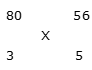
(56 – X): (X – 80) = 3: 5
280 – 5X = 3X – 240
8X = 520
X = 65
Average speed of journey = 65 km/h
Note: After applying the concept of alligation on speed on different parts of the journey we will get the ratio of time taken to cover those parts.
Example 6: A distance of 360 km can be covered in 6 hours when some part of the journey is covered with speed 45 km/h and remaining with speed 90 km/h, then find the distance covered with speed 45 km/h.
Solution:
Average speed of the journey = 360/6 = 60 km/h
By the rule of alligation:
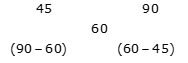
Ratio of time taken = 30: 15 = 2: 1
Time for which journey is covered with speed 45 km/h = 6 * (2/3) = 4 hours
Distance covered by 45 km/h speed = 45 * 4 = 180 km
Attempt a FREE RRB NTPC Mock Here
Alligation in Simple/Compound Interest Problems
The concept of alligation can be applied to SI and CI if we can calculate the effective interest rate for given time period.
For example:
Equivalent of 20% SI for 3 years = 20% * 3 = 60%
Equivalent of 20% CI for 2 years = [(1.2)2 – 1] * 100 = 44%
Example 7: Rahul lent Rs.5000 to Sumit at 25% SI for 2 years and borrowed Rs.3000 from Suresh for 3 years 10% SI, then find the profit/loss on interest amount of Rahul.
Solution:
Effective rate of interest for 2 years on lent amount = 25% * 2 = 50%
Effective rate of interest for 3 years on borrowed amount = -10% * 3 = -30% [Negative because interest will be given.]
By the rule of alligation:
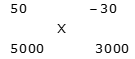
(-30 – X): (X – 50) = 5000: 3000 = 5: 3
-90 – 3X = 5X – 250
8X = 160
X = 20
Hence, total profit on interest amount = 20% of (5000 + 3000) =
= Rs.1600
Note: After applying the alligation concept in effective interest rate we will get the ratio of amount invested.
Example 8: Ronit invested a certain amount in scheme A for 2 years at 10% annual CI and the remaining amount in scheme B for 3 years at 20% annual CI. If the total interest amount received by him is 41.72% of the total invested amount, then find the ratio of the invested amount in scheme A to that in scheme B.
Solution:
Effective interest rate for 2 years on scheme A = [(1.1)2 – 1] * 100 = 21%
Effective interest rate for 3 years on scheme B = [(1.2)3 – 1] * 100 = 72.8%
By the rule of alligation:
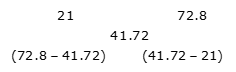
Ratio of amount invested in scheme A to B = 31.08: 20.72
= 3: 2
Alligation in Average, Ratio, and Percentage Problems
By applying the rule of alligation we can solve the problems of averages, ratios, and percentages quickly.
Example: 9: Average age of a 25 students of a class is 24 years and average age of remaining 15 students of the class is 18 years, then find the average age of the class.
Solution:
Let average age of class = A
By the rule of alligation:
(18 – A): (A – 24) = 25: 15 = 5: 3
54 – 3A = 5A – 120
8A = 174
A = 21.75
Hence, average age of the class = A = 21.75 years
Example 10: Ratio of marks obtained to maximum marks by Arun in math and English is 5: 3 and 3: 1. If maximum marks in both the subjects are same, then find the ratio of marks obtained to maximum marks by Arun when both the subjects are taken together.
Solution:
By the rule of alligation:
(3/4 – A): (A – 5/8) = 1: 1
3/4 – A = A – 5/8
2A = 11/8
A = 11/16
Required ratio = 11: (16 – 11) = 11: 5
Example 11: In states A and B out of the total population, the male population is 60% and 50% respectively. If the male population, when both the states are taken together, becomes 58% of the total population, then find that total population of state B is what percent of that of state A.
Solution:
By the rule of alligation:
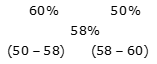
Ratio of total population of state A to that of state B = -8: -2 = 4: 1
Required percent = (1/4) * 100
= 25%
We hope you have got an idea of the topic and can start practicing questions of mixture and alligation.
Stay connected for more topics.
All the best.
Some Useful Links
For Free Practice Questions Register here.
For High-Level DI Questions, Register here.
Solve DI based on Time and Work Here
How to Master Quants section – Know Here!
Attempt Various Free Mock Tests Here: Topic Tests, Sectional Tests, and Full Mock Tests.
Study at your own convenience anywhere. Download the Oliveboard app now!
Oliveboard is a learning & practice platform for premier entrance exams. We have helped over 1 crore users since 2012 with their Bank, SSC, Railways, Insurance, Teaching and other competitive Exams preparation.
Oliveboard Live Courses & Mock Test Series
