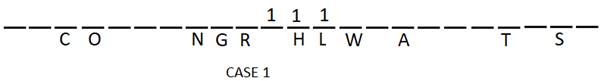There is an odd number of columns of boxes such that each column has three boxes stacked one above the another except the three columns which have one box each. The columns having one box each are placed exactly in the middle of the row.
Three columns are in between columns N and O. Column C is fifth to the left of column N.
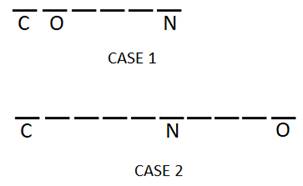
Column G is adjacent to column N. More than six boxes are in between columns G and O. So, O and G cannot be towards the same side of N. Column H is third to the right of column G.
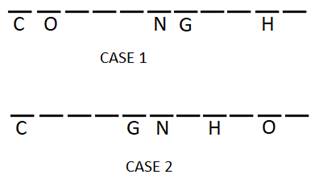
Three columns are in between columns A and H. There are three boxes in between columns A and W such that W is to the left of A. So, either 3 columns of 1 box each or 1 column of 3 boxes will be in between W and A.
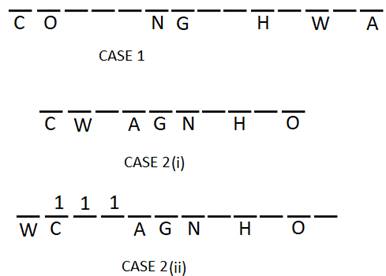
There are three boxes in between columns W and R. In case 1 as there are 3 boxes in between W and A, so R will be to the left of W and there will be 3 columns of 1 box each in between W and R. There are six boxes in between columns L and A.
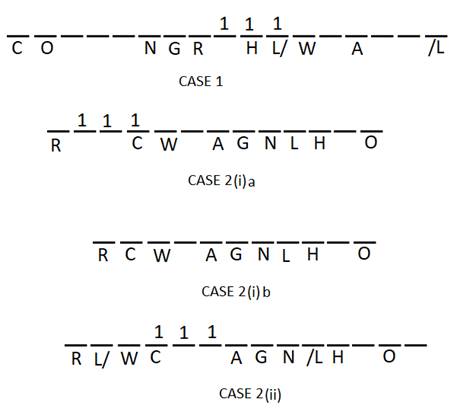
Column T is to the right of column A. As many columns are in between columns A and T as that in between columns N and H. So, cases 2(i)a,2(i)b and case 2(ii) are invalid. Column L is not adjacent to column T.
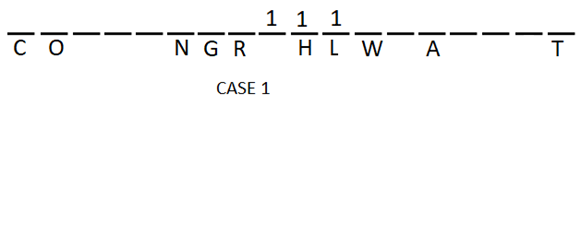
There are three boxes in between columns S and T. There is only one column to the right of column S. As many columns are to the right of column T as that to the left of column O.
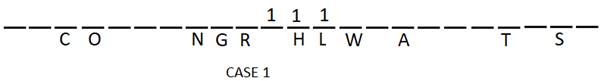
So, there are 23 columns of boxes.
6 boxes are to the left of C.
Study Notes
Category
