Previous Year Questions

The total number of people who like English = 2 (e + c + f + g) - 1050

The number of people who like only Hindi = 2X - 300

1200 = 2X - 300

X = 750

Let the number of people who like Hindi and Biology but not English to the number of students who like Hindi and English but not Biology be 49h: 66h respectively.

The number of people who like Hindi and Biology but not English = a + c + e = 49h

The number of students who like Hindi and English but not Biology = a + b + d = 66h

The total number of people who like only Biology = c

The number of people who like only English = c + X + 250 = c + 1000

The number of people who like all three subjects (English, Hindi, Biology) = g

(c + c + 1000) * 2/13 = g

The number of students who like only Hindi and Biology = d + 150 = 49h - 1200 - c

The number of students who like only Hindi and English = d = 66h - 1200 - c - 1000

Who likes only Hindi and Biology - Who likes only Hindi and English = 150

49h - 1200 - c - 66h + 1200 + c + 1000 = 150

17h = 850

h = 50

The number of students who like Biology = 1900

49h - 1200 + 250 + (2c + 1000) * 2/13 = 1900

49 * 50 - 950 + (2c + 1000) * 2/13 = 1900

1500 + (2c + 1000) * 2/13 = 1900

(2c + 1000) * 2/13 = 400

2c + 1000 = 2600

c = 800

Only English = c + 1000 = 800 + 1000 = 1800 (b)

Only Hindi and Biology = 49 * 50 - 1200 - 800 = 450 (e)

Only Hindi and English = 450 - 150 = 300 (d)

All three subjects = (2c + 1000) * 2/13

= (2 * 800 + 1000) * 2/13

= 400 (g)

Who like Hindi = a + d + e +g

Y + 700 = 1200 + 300 + 450 + 400

Y = 1650

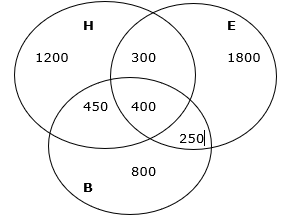
The total number of students who like only Hindi, only English, and only Biology = 1200 + 1800 + 800

= 3800