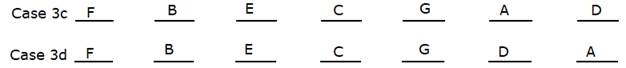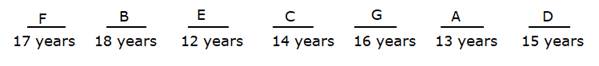Seven persons A, B, C, D, E, F and G sit on the chairs arranged in a linear row from left to right end.
They all are facing in the north direction.
The distance (in meters) between persons is related to their ages. Their ages are 12, 13, 14, 15, 16, 17 and 18 years.
Note: The length of each chair is negligible.
F sits fourth to the left of G. Neither F nor G is a neighbour of E.
E does not sit at extreme ends. So, case 1 and case 3a are invalid.
A, who sits towards the right of C and E, is the neighbour of D. Thus, case 1a and case 2 are invalid.
Atleast three people sit between B and D.
Thus, case 3 and case 3b are invalid.
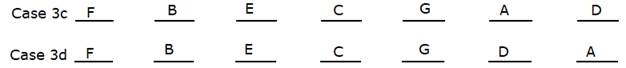
The distance towards the right of A's chair is twice of his age. Thus, case 3d is invalid.
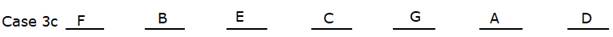
The ages of A and F are prime numbers where only B is elder than F.
Only two persons are younger than C.
| Ages (in years) | Persons |
| 12 | |
| 13 | A |
| 14 | C |
| 15 | |
| 16 | |
| 17 | F |
| 18 | B |
D's age is an odd number.
E is younger than G.
| Ages (in years) | Persons |
| 12 | E |
| 13 | A |
| 14 | C |
| 15 | D |
| 16 | G |
| 17 | F |
| 18 | B |
Therefore, we get:
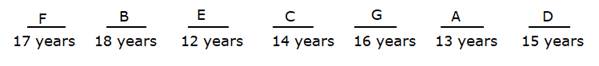
The distance towards the left of B's chair is thrice of his age.
The distance towards the right of A's chair is twice of his age.
The distance between D and G is twice of D's age.
The distance between C and G is the sum of their ages.
The distance between C and F is 105m, whereas the distance between C and E is twice of G's age.
G's age = 16 years. So, distance between C and E is 32m.
Therefore, the final arrangement is:
Only B and F are elder than G.
F sits second to the left of E.
B sits second from the west end of a row.
Study Notes
Category
