Previous Year Questions

(i) Given, PQ=QR,

Therefore, ΔPOR is an isosceles triangle.

Hence, statement (i) is correct.

(ii) The centroid of a triangle is the point of intersection of all the three medians of a triangle.

When we draw, line PO to point S on side QR and S is not mid-point.

So, QS ≠ SR.

Hence, O is not the centroid of ΔPQR.

Hence, statement (ii) is not correct.

(iii) ΔPQO is congruent to ΔRQO.

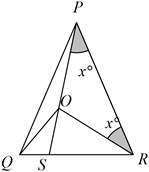
Given PQ = QR

And ∠OPR=∠ORP So, PO = OR

In ∆PQO and ∆RQO,

PQ = RQ

And PO = RO

QO = QO (common side)

Hence, ΔPQO is congruent to ΔRQO.

Hence, statement (iii) is correct.